Multiple Linear Regression

จากบท Simple Linear Regression เราคงรู้ว่าเมื่อตัวแปร x และ y มีความสัมพันธ์กัน (correlation) เราสามารถสร้างโมเดลถอดถอยในการทำนาย (predict) ได้

แต่บางครั้ง ตัวแปร x อาจจะมีหลายตัว เพราะบนโลกความเป็นจริง เราอาจต้องเก็บข้อมูลตัวแปรต่าง ๆ ที่เข้ากับโมเดลในทฤษฎีของเรา

บทเรียนนี้เราจะมาพูดถึงความสัมพันธ์ของ x1, x2 ที่มีต่อตัวแปร y กัน

y^ = α + βx + ε
α หมายถึง y-intercept หรือ จุดที่ข้อมูลตัดบนแกน y
β หมายถึง ความชันของตัวแปร x
ε หมายถึงerror ในโมเดล

ถ้าหากเรามีตัวแปร x 2 ตัว สมการจะเขียนได้ดังนี้

y^ = α + βx1 + βx2 + ε

โดยการวิเคราะห์ Multiple Regression จะมีข้อตกลงเบื้องต้นไม่ต่างจาก Simple Regression

Linear relationship : คือ x และ y มีแนวโน้มที่จะเป็นเส้นตรง

Independence : คือการที่ residuals (ค่าหลงเหลือจากการขีดเส้นตรง) มีความแยกออกจากัน

Homoscedasticity : คือการที่ residuals มีความสม่ำเสมอในทุก ๆ ช่วงของ x

Normality : คือการที่ residuals มีโค้งปกติ Note* อันนี้คือค่า residuals ไม่ใช่ค่าข้อมูลนะ

Multi-collinearity : คือการที่ตัวแปร x มีความสัมพันธ์กันสูง จะทำให้ผลที่ได้มีความอคติ

แต่จะมีเพิ่มข้อตกลงเบื้องต้น 1 ข้อ เรียกว่า Multi-collinearity

แต่สำหรับการวิเคราะห์ใน R เราจำเป็นต้องเขียนสมการโมเดลก่อน ด้วยคำสั่ง lm(y ~ x1 + x2, data)

ในตัวอย่างนี้ เราจะใช้ data ที่เราสร้างขึ้น เรื่อง น้ำหนัก ชั้นเรียน และจำนวนกาแฟเฉลี่ยที่ดื่ม เหมือนเดิม

Grade <- 1:12
Avg_weight <- c(48, 54, 61, 69, 74, 85, 89, 99, 110, 100, 114, 150)
Avg_coffee <- c(6, 7, 1, 0, 4, 6, 4, 4, 7, 7, 7, 7)
data <- data.frame(Grade, Avg_weight, Avg_coffee)
head(data)

##   Grade Avg_weight Avg_coffee
## 1     1         48          6
## 2     2         54          7
## 3     3         61          1
## 4     4         69          0
## 5     5         74          4
## 6     6         85          6

# เขียนโมเดล

model_multiple <- lm(Avg_weight ~ Grade + Avg_coffee, data = data)

ทดสอบ Assumptions

• ทดสอบ Linear relationship

car::crPlots(model_multiple)

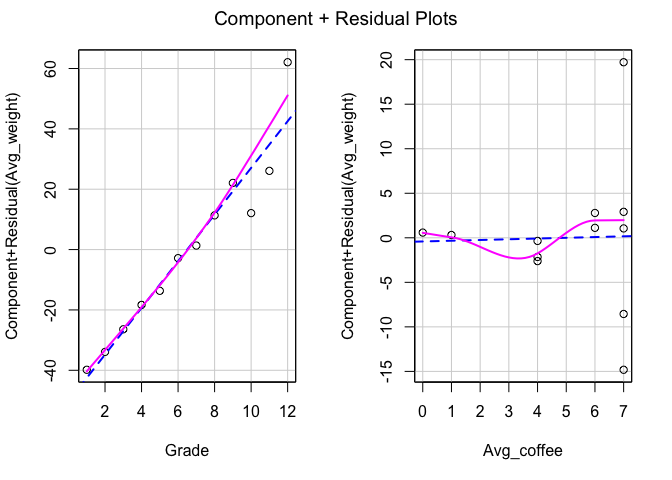
car::ncvTest(model_multiple)

## Non-constant Variance Score Test 
## Variance formula: ~ fitted.values 
## Chisquare = 10.19174, Df = 1, p = 0.0014107

• ทดสอบ Homoscedasticity

plot(model_multiple, 3)

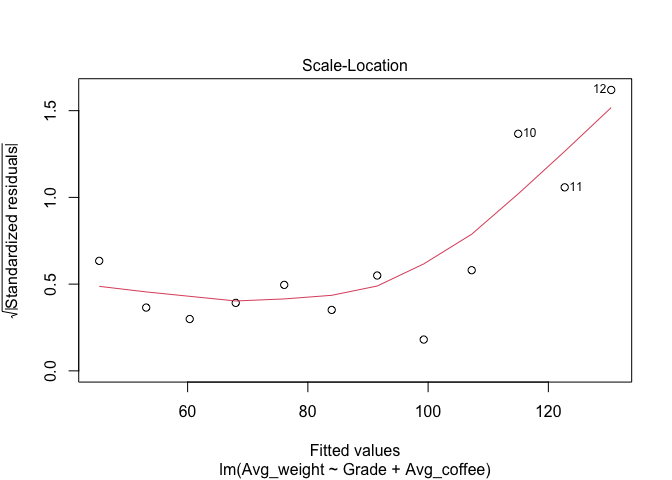
• ทดสอบ Normality

car::qqPlot(model_multiple)

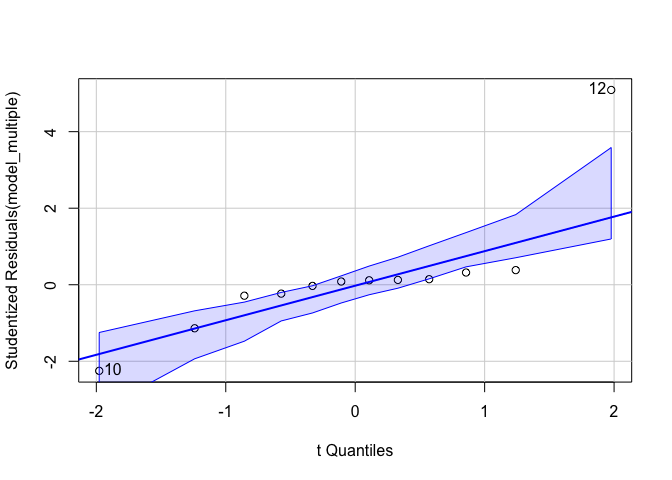
    ## [1] 10 12

• ทดสอบ Multi-collinearity จะทดสอบด้วย vif()

car::vif(model_multiple)

    ##      Grade Avg_coffee 
    ##   1.243642   1.243642

ปกติแล้วเราจะอนุญาตให้ vif มีค่าไม่เกิน 2.5 ถ้ามากกว่านั้น โดยเฉพาะมากกว่า 5.00 จะเรียกว่ามีความสัมพันธ์ที่ทับซ้อนกันเกินไป

---

การวิเคราะห์และอ่านผล Multiple Regression

เนื่องจากเราเขียนโมเดลด้วยคำสั่ง lm() ออกมาแล้ว และข้อตกลงเบื้องต้นไม่ได้ถูกละเมิดมากนัก ต่อไปเราจะวิเคราะห์ด้วยสมการถดถอยพหุและอ่านผลกันค่า

model_multiple <- lm(Avg_weight ~ Grade + Avg_coffee, data = data)
summary(model_multiple)

## 
## Call:
## lm(formula = Avg_weight ~ Grade + Avg_coffee, data = data)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -14.9837  -2.1836   0.7683   1.4520  19.5484 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 37.06717    6.61555   5.603 0.000333 ***
## Grade        7.73396    0.82921   9.327 6.37e-06 ***
## Avg_coffee   0.08242    1.22057   0.068 0.947638    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 8.892 on 9 degrees of freedom
## Multiple R-squared:  0.9237, Adjusted R-squared:  0.9067 
## F-statistic: 54.44 on 2 and 9 DF,  p-value: 9.387e-06

จะเห็นได้ว่าผลจะมีความแตกต่างจากผล simple regression ไม่มากนัก แต่มีตัวแปรขึ้นมาเพิ่ม ดังนั้น สมการของโมเดลนี้ คือ

Y^ = intercept + coefx1(x1) + coefx2(x2) + e

เมื่อนำผลเข้าไปอยู่ในสมการแล้วจะพบว่า

Y^ = 37.07 + 7.73(Grade) + 0.08(Avg_coffee) + e

อ่านผลได้ ดังนี้

• เมื่อไม่สนใจตัวแปร Grade และ Avg_coffee แล้ว ค่าเฉลี่ยของ Avg_weight จะอยู่ที่ 37.07

• เมื่อ Grade เพิ่มขึ้น 1 ปี จะทำให้ค่า Avg_weight เพิ่มขึ้น 7.73 กิโลกรัม อย่างมีนัยสำคัญทางสถิติ (เมื่อให้ Avg_coffee คงที่)

• เมื่อ Avg_coffee เพิ่มขึ้น 1 แก้ว จะทำให้ค่า Avg_weight เพิ่มขึ้น 0.08 แต่ไม่มีนัยสำคัญทางสถิติ (เมื่อให้ Grade คงที่)

• และโมเดลนี้สามารถอธิบายตัวแปรตามได้ 92.37 เปอร์เซ็นต์ และเมื่อทดสอบด้วย F-test พบนัยสำคัญทางสถิติ p < 0.001

ลูกแมวอาจจะถึงขั้นถอดใจเมื่อมาถึงจุดนี้ แต่อาจสรุปว่าตัวแปรที่ทำให้น้ำหนักเฉลี่ยเพิ่มขึ้นคือชั้นปี

โปรดระวัง คำว่า “ทำให้” เพราะมันไม่ได้ทำให้ค่าข้อมูล Y ที่เราเก็บมาเพิ่มขึ้น แต่มันทำให้ Y^ หรือ Y ทำนายเพิ่มขึ้นจ้า

Plot graph เป็นกิจวัตร

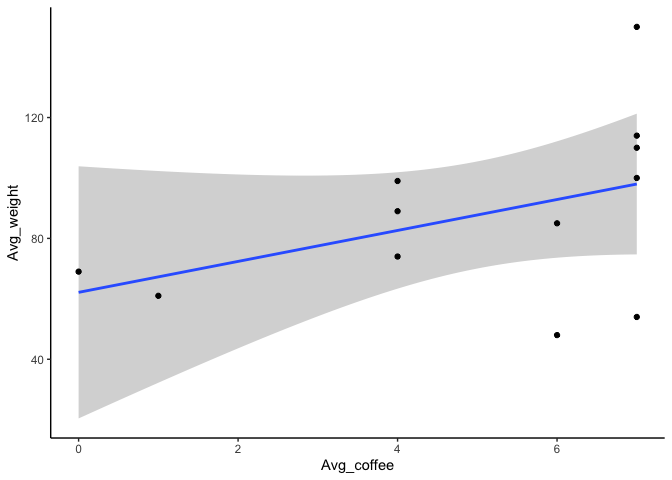
ใช้ ggplot2 แบบแยกตัวแปร

library(ggplot2)

ggplot(data, aes(x = Avg_coffee, y = Avg_weight)) +
  geom_smooth(method = lm) +
  geom_point(stat = "identity") +
  theme_classic()

ggplot(data, aes(x = Grade, y = Avg_weight)) +
  geom_smooth(method = lm) +
  geom_point(stat = "identity") +
  theme_classic()